What Is Proper Subset In Math
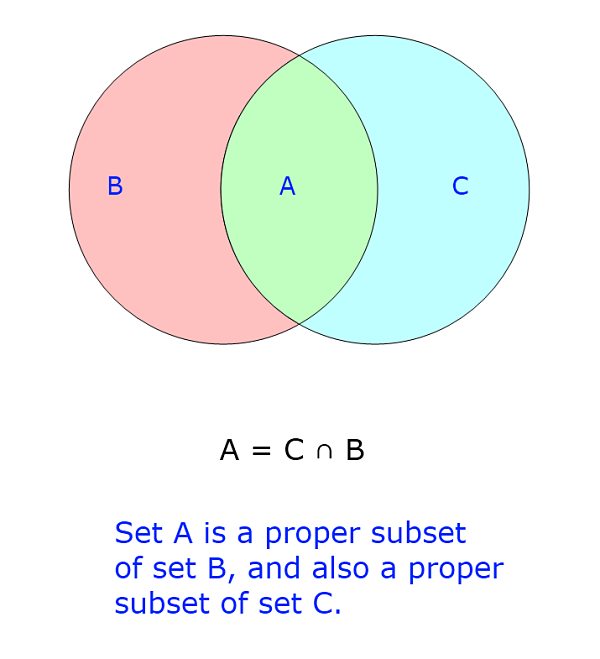
What Is Proper Subset In Math - In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. If a is a subset of b (a ⊆ b), but a is not equal to b, then we say a is a proper subset of b, written as a ⊂ b or a ⊊ b. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. In other words, if b is a proper subset of a, then all elements of b are in. The following diagram shows an. A proper subset of a set a is a subset of a that is not equal to a.
The following diagram shows an. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. A proper subset of a set a is a subset of a that is not equal to a. In other words, if b is a proper subset of a, then all elements of b are in. If a is a subset of b (a ⊆ b), but a is not equal to b, then we say a is a proper subset of b, written as a ⊂ b or a ⊊ b. In other words, if b is a proper subset of a, then all elements of b are in a but a contains at.
The following diagram shows an. A proper subset of a set a is a subset of a that is not equal to a. In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. In other words, if b is a proper subset of a, then all elements of b are in. If a is a subset of b (a ⊆ b), but a is not equal to b, then we say a is a proper subset of b, written as a ⊂ b or a ⊊ b.
What Do Subsets Mean in Statistics? Outlier
If a is a subset of b (a ⊆ b), but a is not equal to b, then we say a is a proper subset of b, written as a ⊂ b or a ⊊ b. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. A proper subset.
rmstart Blog
In other words, if b is a proper subset of a, then all elements of b are in. In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. In set theory, a proper subset of a set a is a subset of a that cannot be equal.
Algorithms Proper subset (meaning) YouTube
If a is a subset of b (a ⊆ b), but a is not equal to b, then we say a is a proper subset of b, written as a ⊂ b or a ⊊ b. A proper subset of a set a is a subset of a that is not equal to a. In other words, if b is.
Introduction to Subsets (new version available) YouTube
In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. The following diagram shows an. In other words, if b is a proper subset of a, then all elements of b are in. If a is a subset of b (a ⊆ b), but a is not.
Proper subset vs subset Math, Math equations, Theories
The following diagram shows an. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. In other words, if b is a proper subset of a, then all elements of b are in. In other words, if b is a proper subset of a, then all elements of b.
Proper and Improper Subsets Set Theory Examples YouTube
A proper subset of a set a is a subset of a that is not equal to a. The following diagram shows an. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. In other words, if b is a proper subset of a, then all elements of b.
PPT Section 2.2 Subsets PowerPoint Presentation, free download ID
In other words, if b is a proper subset of a, then all elements of b are in. In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. The following diagram shows an. A proper subset of a set a is a subset of a that is.
PPT Section 2.2 Subsets PowerPoint Presentation, free download ID
In other words, if b is a proper subset of a, then all elements of b are in. In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. The following diagram shows an. A proper subset of a set a is a subset of a that is.
Discrete Mathematics Unit 1 Set Theory and Logic
In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. In other words, if b is a proper subset of a, then all elements of b are in a but a contains at. If a is a subset of b (a ⊆ b), but a is not equal to.
BASIC INTRODUCTION PROPER SUBSETS WITH EXAMPLE OF KIDS MATH
In other words, if b is a proper subset of a, then all elements of b are in. In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. The following diagram shows an. If a is a subset of b (a ⊆ b), but a is not equal to.
A Proper Subset Of A Set A Is A Subset Of A That Is Not Equal To A.
In set theory, a proper subset of a set a is a subset of a that cannot be equal to a. In other words, if b is a proper subset of a, then all elements of b are in. The following diagram shows an. If a is a subset of b (a ⊆ b), but a is not equal to b, then we say a is a proper subset of b, written as a ⊂ b or a ⊊ b.