Do Two Vertical Angles Form A Linear Pair

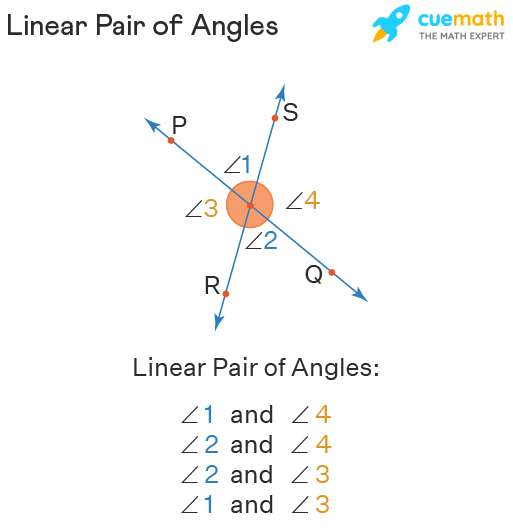
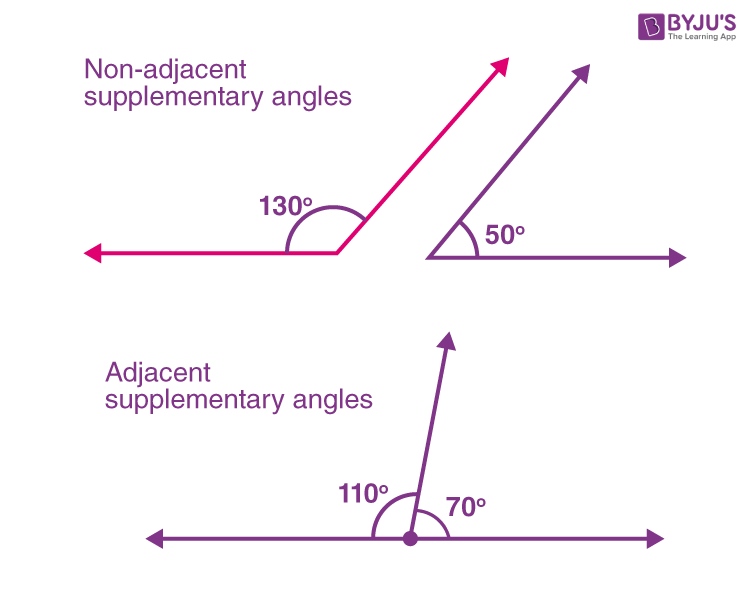
Do Two Vertical Angles Form A Linear Pair - A linear pair cannot be formed by a pair of vertical angles. The given statement is false. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. A linear pair is a pair of two angles that are adjacent and supplementary. Let’s quickly go over the definitions what it means to be adjacent. When two lines cross, vertical angles are. A linear pair is two adjacent. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180.

A linear pair is two adjacent. Let’s quickly go over the definitions what it means to be adjacent. When two lines cross, vertical angles are. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair cannot be formed by a pair of vertical angles. A linear pair is a pair of two angles that are adjacent and supplementary. The given statement is false. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines.

When two lines cross, vertical angles are. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. A linear pair is a pair of two angles that are adjacent and supplementary. Let’s quickly go over the definitions what it means to be adjacent. A linear pair is two adjacent. The given statement is false. A linear pair cannot be formed by a pair of vertical angles.

What are Vertical Angles? — Mashup Math

A linear pair cannot be formed by a pair of vertical angles. A linear pair is a pair of two angles that are adjacent and supplementary. The given statement is false. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 =.

Which Pair Of Angles Are Vertical Angles

Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair is two adjacent. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. A linear pair is a pair of two.

Question 1 In the figure (i) Is angle 1 adjacent to 2? (ii) Is AOC

A linear pair is two adjacent. Let’s quickly go over the definitions what it means to be adjacent. A linear pair is a pair of two angles that are adjacent and supplementary. A linear pair cannot be formed by a pair of vertical angles. When two lines cross, vertical angles are.

What are Vertical Angles? — Mashup Math

The given statement is false. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. Let’s quickly go over the definitions what it means to be adjacent. When two lines cross, vertical angles are. A linear pair cannot be formed.

Two angles form a linear pair. The measure of one CameraMath

A linear pair is two adjacent. A linear pair cannot be formed by a pair of vertical angles. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. A linear pair is a pair of two angles that are adjacent.

Two angles forming a linear pair are always

A linear pair is two adjacent. The given statement is false. A linear pair cannot be formed by a pair of vertical angles. When two lines cross, vertical angles are. Let’s quickly go over the definitions what it means to be adjacent.

Linear Pair of Angles Definition, Axiom, Examples

When two lines cross, vertical angles are. A linear pair is a pair of two angles that are adjacent and supplementary. A linear pair is two adjacent. The given statement is false. Let’s quickly go over the definitions what it means to be adjacent.

What Is Vertical Angles Theorem Nelson Bountly

The given statement is false. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4 = 180. When two lines cross, vertical angles are. A linear pair is a pair of two angles that are adjacent and supplementary. Let’s quickly go over.

Example of supplementary angle chlistmuscle

The given statement is false. Let’s quickly go over the definitions what it means to be adjacent. Vertical angles are a pair of nonadjacent angles, ∠1 and ∠2, formed by two intersecting lines. A linear pair cannot be formed by a pair of vertical angles. A linear pair is a pair of two angles that are adjacent and supplementary.

Day 1 HW Angle Pairs Adjacent, vertical, supplementary, complementary

A linear pair is a pair of two angles that are adjacent and supplementary. A linear pair is two adjacent. Let’s quickly go over the definitions what it means to be adjacent. Vertical angles, such as ∠1 and ∠2, form linear pairs with the same angle, ∠4, giving m ∠1 + m∠4 = 180 and m ∠2 + m ∠4.

A Linear Pair Cannot Be Formed By A Pair Of Vertical Angles.

Let’s quickly go over the definitions what it means to be adjacent. When two lines cross, vertical angles are. A linear pair is a pair of two angles that are adjacent and supplementary. A linear pair is two adjacent.